Mavi Beyin Projesi: 11 Boyutlu Evren Nöronlarınızın Arasında
2018 yılında nörobilimciler
beynimizin yapısını anlayabilmek için yenilikçi bir şekilde klasik bir
matematik dalı olan cebirsel topolojiyi kullandılar.
Bunun sonucunda da beynin 11 boyutta faaliyet
gösteren çok boyutlu geometrik yapılarla dolu olduğunu buldular.
Ancak konuya başlamadan önce kısaca topoloji nedir onu anlayalım;
Topoloji Nedir?
Topoloji; yüzeylerin ve genel şekillerin özelliklerini inceleyen, fakat uzunluk ve açılarla ilgilenmeyen geometri dalıdır. Önem verdiği şeylerin başında şekillerin başka bir şekle dönüştüklerinde değişmeyen özellikleri gelir. Şekilleri dilediğimiz gibi çekiştirmek serbesttir, hatta bu yüzden topolojiye bazen “lastik levha geometrisi” denir.

Kaynak: www.matematiksel.org
Normalde bir yüzeyin iki tarafı olur. Bir topun dışıyla içi farklı yüzlerdir; bir yüzden öbürüne geçmek için delik açmak gerekir ki topolojide bu gibi işlemlere izin yoktur (çekmek serbest ama kesmek yok ). Tek taraflı bir yüzeyin nasıl olabileceğini ilk başta aklımız almasa da Alman matematikçi ve gökbilimci August Möbius, 19. yüzyılda böyle bir şekil keşfetti. Bu şekli elde etmek için yapmanız gereken bir kağıt şeridi alıp bir ucunu bir tur döndürerek diğer ucuyla birleştirmektir. Oluşan tek taraflı ve tek kenarlı kıvrık şekle “Möbius şeridi” denir. Bir kalemle Möbius şeridinin ortasından itibaren çizmeye başlarsanız başlangıç noktasına dönebilirsiniz.

Kaynak: ResearchGate
Mavi Beyin Projesi
Mavi Beyin projesi ekibi, insan beyninin karmaşıklığını açıklayabilecek ilginç bir fikir ileri sürdü. Karmaşık bağlantıları grafiklere döken matematiksel bir dal olan cebirsel topoloji kullanan araştırmacılar, nöral ağların yapısından karmaşık fonksiyonlar elde edebilecekleri bir yol buldu. Araştırmacılar, fiziksel olarak 3 boyutlu uzayda bulunan beynin içsel bağlantılarının matematiksel karmaşıklığını ifade edecek topolojik uzayın bazen 7 ya da 11 boyutlu olması gerektiğini belirtiyorlar. Yani nöral bağlantıların karmaşıklığı sanılanın çok ötesinde ama yine de onları tanımlayacak bir dile sahip olunabilir.
Topolojik dilde “boyut” sözcüğü karmaşıklığı tanımlamak için kullanılıyor. Singularity Hub’a konuşan, EPFL(École Polytechnique Fédérale de Lausanne)’den lisansüstü öğrencisi Max Nolte şöyle diyor; “Çalışmamızda boyut sözcüğü, uzay boyutlarını tanımlamıyor; açıklamak istediğimiz geometrik nesnelerin topolojik boyutunu tanımlıyor. 7 veya 11 boyutlu simpleksler halen üç boyutlu fiziksel uzayda yerleşik olarak bulunuyor”. Yani burada boyut sözcüğü, simplekslerin karmaşıklığını anlatıyor.
Bu model, kendilerini insan beyninin süper bilgisayar destekli bir modellemesini inşa etmeye adamış bir İsviçre araştırma girişimi olan Mavi Beyin Projesi’nde yer alan sinirbilimciler ve matematikçilerden oluşan bir araştırma ekibi tarafından üretildi. Çalışmaları, benzeri görülmemiş miktarda ayrıntıyı kapsayan ve 12.000 nöronu simüle eden bir sinir devresinin bilgisayar modeline dayanıyor. EPFL bilim insanı Sean Hill; “Beyin dalgalarının altında yatan özellikleri incelemek için ilk kez bu karmaşıklıkta bir model kullanıldı” diyor. “Bilgisayar modeline ihtiyacımız var, çünkü potansiyel olarak milyarlarca bireysel nöronun elektriksel aktivitesini ve bunun sonucunda ortaya çıkan beyin dalgalarını ilişkilendirmek imkansız.” “Bu görüş aracılığıyla laboratuvarda incelenen beyin dokusundan ölçülen beyin dalgalarını tek nöron seviyesinde yorumlayabiliriz.”
Beyin Dalgaları Nasıl Oluşur?
Nöronlar aslında minik bir pil gibidir, “spike” olarak bilinen elektriksel uyarıları ateşlemek için şarj edilmeleri gerekir. Nöronlar, bu “spike”lar ile düşünceleri ve algıları üretmek için birbirleriyle iletişim kurarlar. Bir nöronu yeniden şarj etmek için “iyon” olarak adlandırılan yüklü parçacıkların minik iyon kanallarından geçmesi gerekir. Bu kanallar elektrik akımının akışını düzenleyen kapılar gibidir. Sonuçta, nöronların tüm devresi boyunca çoklu elektrik sinyallerinin birikmesi beyin dalgaları üretir.
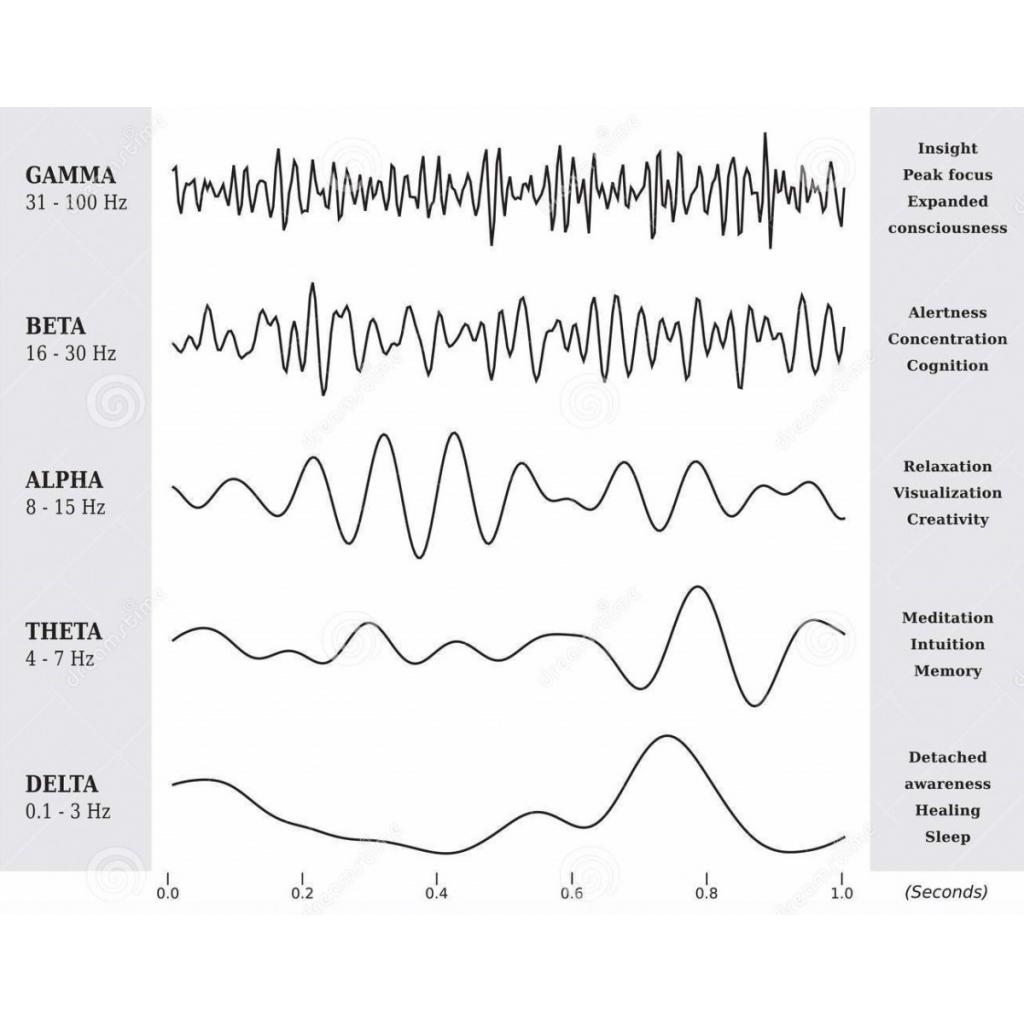
Kaynak: www.dreamstime.com
Neokorteksin Topoloji ile Birleşimi
Mavi Beyin Projesi’nin temel araştırma aracı, 2015’de detaylı bir dijital modeli tamamlanmış ve beynin üst düzey faaliyetlerinden sorumlu olan neokortekstir. Matematikçi olarak EPFL’den Kathryn Hess ve İskoçya’da yer alan Aberdeen Üniversitesi’nden Ran Levi, neokortikal nöronların uyarıldıklarında nasıl çalıştıklarını araştırmak için cebirsel topoloji olarak bilinen karmaşık bir yaklaşım kullandılar. Bunu nasıl yaptıklarına gelirsek;
Ekip, başlarında Lida Kanari ile birlikte neokortekste en sık gözlenen nöronun -piramidal hücrelerin- farklı şekillerini ayırt edebilmek için bir algoritma geliştirdi (Piramidal hücreler; neokorteksteki nöronların % 80’ini oluşturan, antenler gibi beyindeki diğer nöronlardan bilgi toplayan ağaç benzeri hücrelerdir. Bu hücreler eksitatördür; algı, davranış ve hislerimizi nöron ağı üzerinden elektriksel aktivite dalgaları göndererek oluştururlar).
Çoğu nöronun yapısı; diğer nöronlara bağlanan ve elektrik sinyalleriyle iletişim kuran, çok sayıda dal bulunan karmaşık bir ağacı andırır. Nöron yapısının en uzun (kalıcı) bileşenlerini tutar ve daha küçük dalları ayrıştırırsak, ağaç benzeri yapısını bir barkoda -nöronları farklı gruplara ayıracak herhangi bir makine öğrenme algoritması için girdi olarak kullanılabilecek bir matematiksel nesneye- dönüştürebiliriz.
Her nöron sınıflandırma sürecinin ana sorunu ise şu: Farklı görünen iki hücre, yavaş yavaş değişen farklılıkların sürekliliğinin bir parçası mı (Türlerin farklı suşları gibi; örneğin, köpeklerin farklı tipleri) yoksa gerçekten farklı “nöron türleri” mi (Köpek, kedi, fil)? Başka bir deyişle, birbirlerinin ayrık mı yoksa sürekli morfolojik varyasyonları mı? Bu, topolojik sınıflandırma kullanılarak ve her biri kendine özgü “suşları” olan beyin hücrelerinin farklı “türlerini” gruplayarak cevaplanabilir.
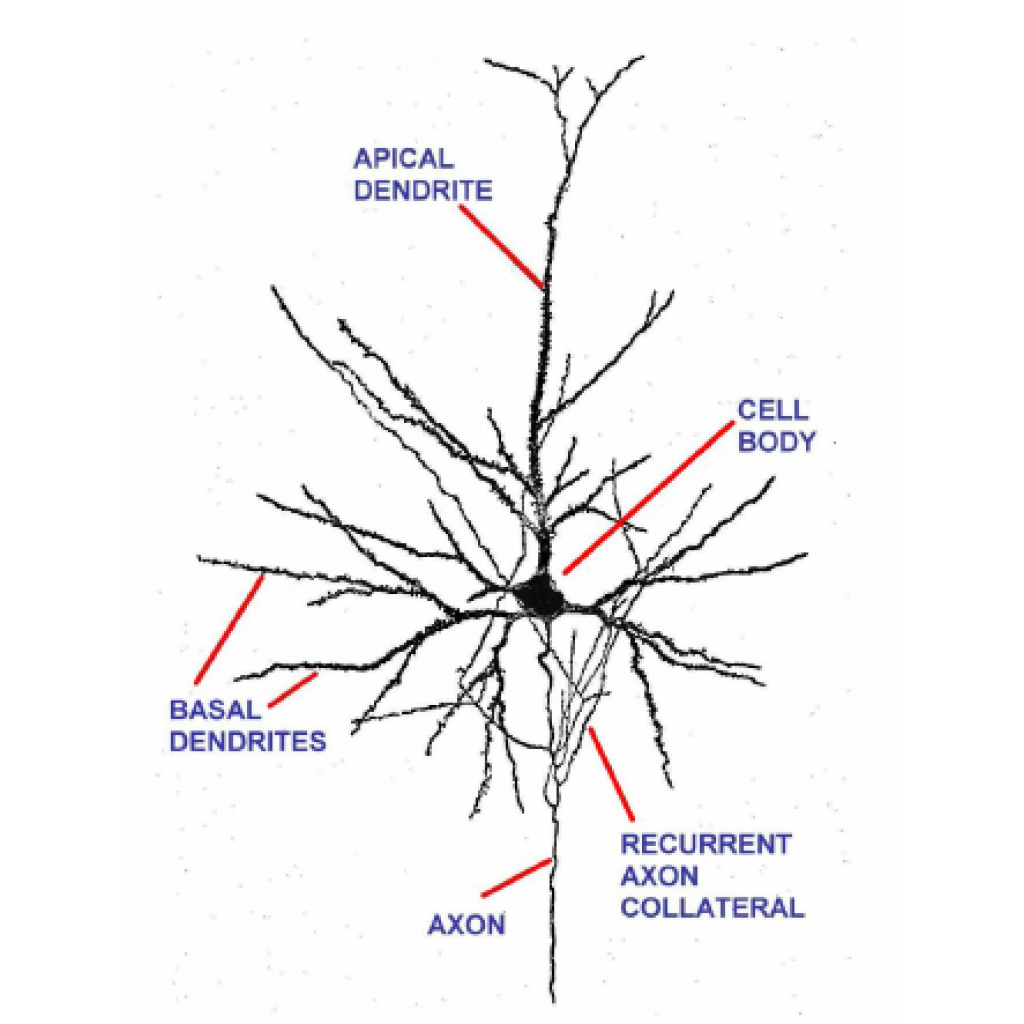
Kaynak: ResearchGate
Hess, cebirsel topoloji hakkında şöyle diyor; “Cebirsel topoloji aynı anda hem teleskop hem de mikroskop kullanmaya benziyor. Aynı anda ağlardaki gizli yapılara da bakabilirsiniz (ormandaki ağaçlar), boşlukları (ağaçsız alanları) da görebilirsiniz.”
Frontiers in Computational Neuroscience dergisinde yayınlanan sonuçlar şaşırtıcıydı; vücuttaki diğer tüm organlardaki hücreler dört boyutta çalışırken – üç uzamsal ve bir zaman – beynin rutin olarak yedi, bazen de on bir kadar boyutta çalıştığı gösterildi. Bu süreç “klik” oluşumu ile başlar (kesin bir nesne oluşturmak için belirli şekillerde birbirlerine bağlanan bir dizi nöron). Mavi Beyin Projesi direktörü Prof. Henry Markram, beynin küçük bir yerinde bile bu nesnelerden on milyonlarcasının olduğunu belirtiyor.
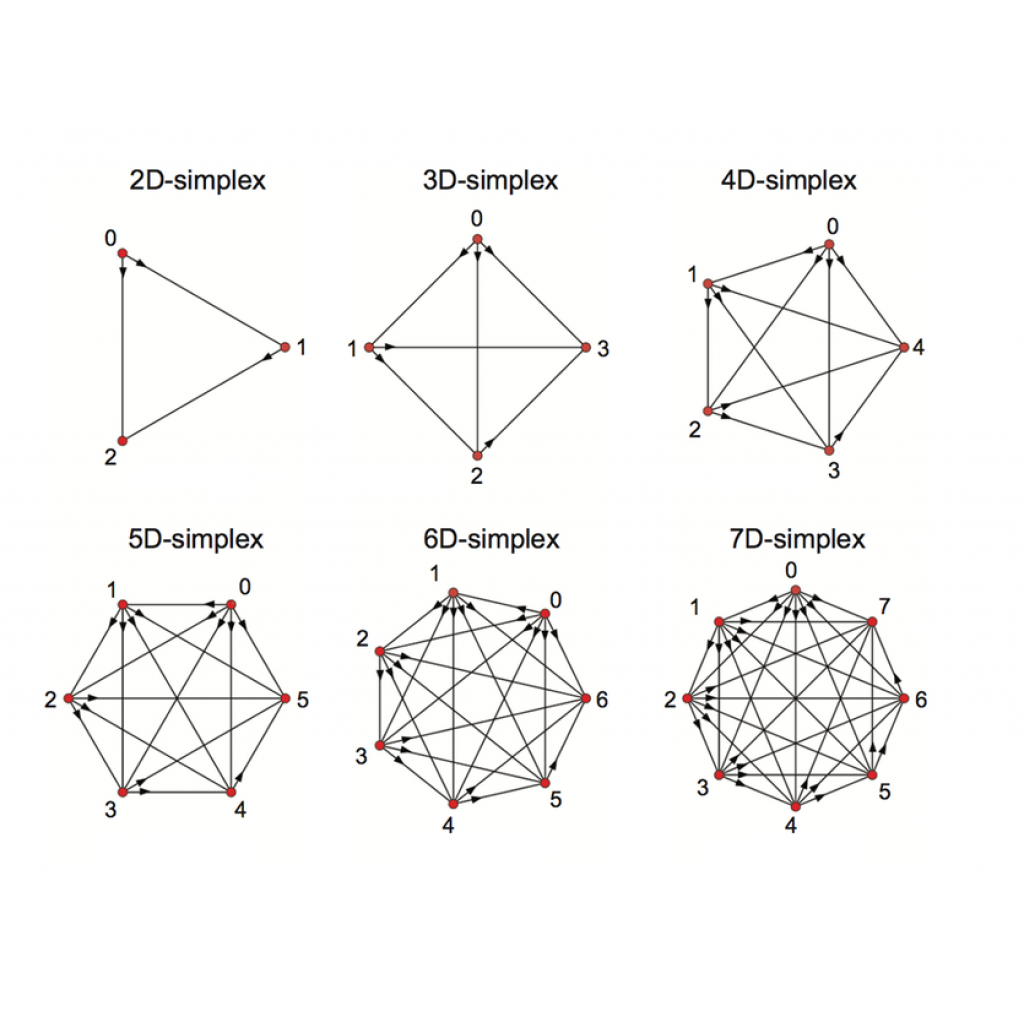
Topolojik olarak konuşan, çok boyutlu “klik”ler oluşturan nöron grupları ve onların aralarındaki bağlantıları temsil eden diyagram.
Kaynak: Mavi Beyin Projesi
Araştırmacılar sanal beyin dokusuna uyaran verdiğinde, gruplar progresif bir şekilde birleşerek anlık olarak en yüksek boyut deliklerine yaklaştılar, yani araştırmacıların bahsettiği boşluklara. Levi şöyle diyor; “Yüksek boyutlu boşlukların görünmesi, beynin nöron ağlarının uyarımı ile bilgiyi işlemesiyle en üst organize olma durumudur. Beyin uyaranla reaksiyona girdiğinde; çubuklardan (1D) desteklere (2D), küplere (3D) ve sonra da çok daha kompleks 4D, 5D cisimlere dönüşüyor. Bu aktivite süreci çok boyutlu “kumdan kale”lere benziyor, sonrasında da kumun ayrışması gibi yeniden çözünüyor”
Mavi Beyin Projesi’nin çözeceği bir sonraki soru, çok boyutlu “kumdan kale”lerin artan karmaşıklığı ile, ilgili sonuçların karmaşıklığı arasında bir bağlantı olup olmadığıdır.
Beyin işlevini haritalamak için cebirsel topolojinin kullanılması hala ilk günlerindedir, ancak yazarlar, bunun beyin fonksiyonunun en büyük gizemlerinden birine bir ipucu vermiş olabileceğini öne sürüyorlar: Hatıraların nerede ve nasıl depolandığı. Markram, “Yüksek boyutlu boşluklarda gizleniyor olabilir ” diyor.
Kaynakça ve ileri okuma için;
- https://www.sciencealert.com/science-discovers-human-brain-works-up-to-11-dimensions
- https://cosmosmagazine.com/mathematics/how-your-brain-works-in-11-dimensions
- https://www.matematiksel.org/topoloji-nedir/
- https://bilimfili.com/beyin-aglarindaki-cok-boyutlu-evren/
- https://www.sciencedaily.com/releases/2017/06/170612094100.htm
- https://www.sciencedaily.com/releases/2019/03/190321130415.htm
- https://www.sciencedaily.com/releases/2013/07/130724124911.htm
- https://www.frontiersin.org/articles/10.3389/fncom.2017.00048/full